
In the world of artificial intelligence, the role of deep learning is becoming important. Artificial intelligence paradigms have traditionally been inspired by the capabilities of the human brain, but deep learning appears to surpass the human brain’s learning capabilities in some ways. Deep learning has undoubtedly made remarkable progress, but it also has drawbacks, such as high computational complexity and the need for large amounts of data.
In light of the above concerns, scientists at Bar-Ilan University in Israel are raising an important question: Should artificial intelligence incorporate deep learning? They published a new paper published in the journal Scientific Reports. This paper continues previous research on the advantages of tree-like architectures over convolutional networks. The main goal of the new research was to find out whether shallow neural networks based on brain-inspired principles could be used to effectively train complex classification tasks while reducing computational load. This article outlines key findings that could reshape the artificial intelligence industry.
Therefore, as we already know, successfully solving complex classification tasks requires training deep neural networks consisting of tens or hundreds of convolutional and fully connected hidden layers. This is quite different from how the human brain works. In deep learning, the first convolutional layer detects local patterns in the input data, and subsequent layers identify larger-scale patterns until reliable class characterization of the input data is achieved.
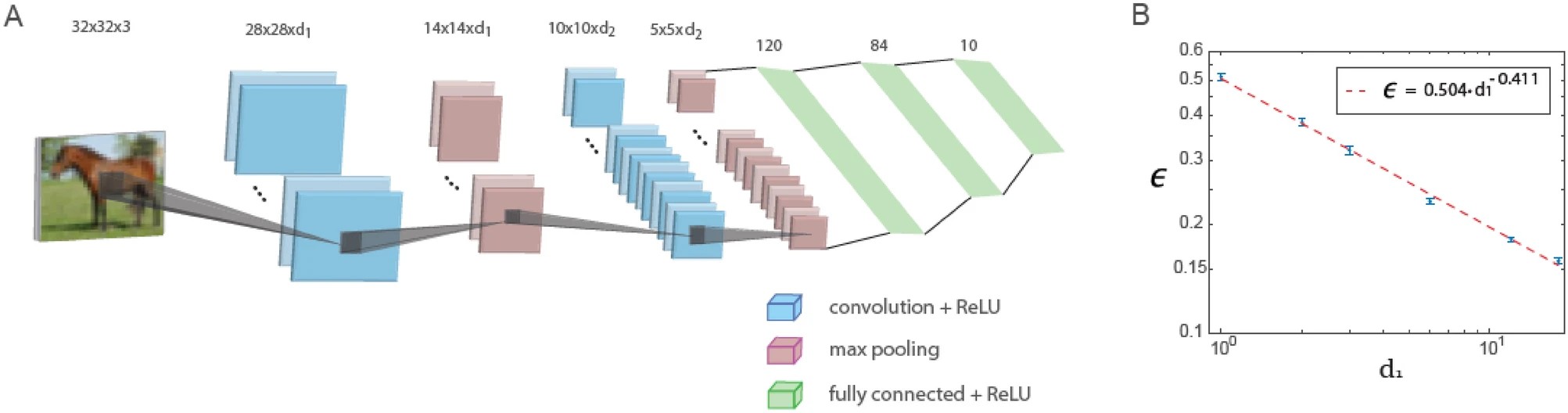
In this study, we show that when using a fixed depth ratio of the first and second convolutional layers, the error of a small LeNet architecture consisting of only five layers decreases with the number of filters in the first convolutional layer according to a power law. Extrapolating this power law shows that the generalized LeNet architecture can achieve low error values similar to those obtained by deep neural networks based on CIFAR-10 data.
The figure below shows training on the generalized LeNet architecture. The generalized LeNet architecture for the CIFAR-10 database (input size 32 x 32 x 3 pixels) consists of five layers. Two convolutional layers with max pooling and three fully connected layers. The first and second convolutional layers contain d1 and d2 filters respectively. Here d1/d2 ≃ 6/16. The plot of the test error, denoted ϵ, shows a power law dependence on d1 and exponent on a logarithmic scale. ρ∼0.41. The neuron activation function is ReLU.

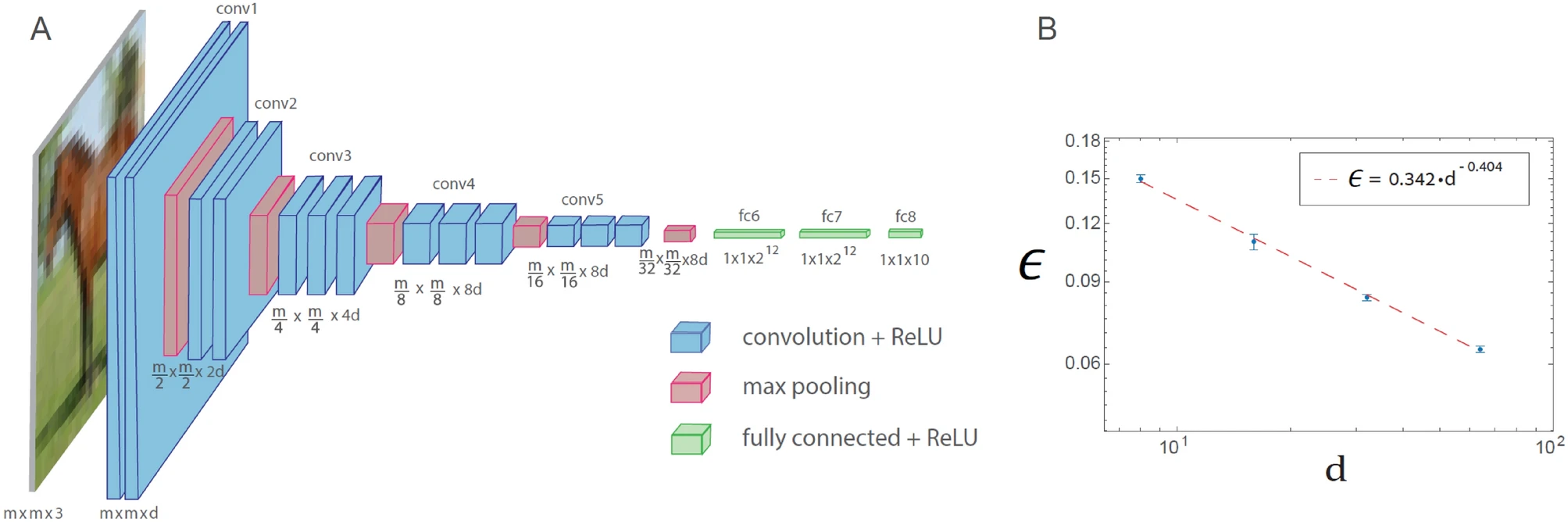
A similar power law phenomenon is observed in the generalized VGG-16 architecture. However, this increases the number of operations required to achieve a given error rate compared to LeNet.
Training of the generalized VGG-16 architecture is shown in the figure below. Generalized VGG-16 architecture consisting of 16 layers. Here the number of filters in the nth convolution set is dx 2n − 1 (n ≤ 4) and the square root of the filter size is mx 2 − (n − 1). (n ≤ 5), where mxmx 3 is the size of each input (d = 64 in the original VGG-16 architecture). A plot of the test error, denoted ϵ, against d on a logarithmic scale for the CIFAR-10 database (m = 32) shows a power-law dependence of the exponent ρ∼0.4. The neuron activation function is ReLU.

Power law phenomena cover a variety of generalized LeNet and VGG-16 architectures, which exhibit universal behavior and suggest quantitative hierarchical complexity in machine learning. It has also been shown that the conservation law of a convolutional layer, equal to the square root of its size multiplied by its depth, minimizes the error asymptotically. The effective approach to surface learning demonstrated in this study will require additional quantitative studies using a variety of databases and architectures, as well as accelerated implementation through specialized hardware designs in the future.


